USAMTS Problem 1/3/13
We will say that an rearrangement of the letters of a word has no fixed letters if, when the rearrangement is placed directly below the word, no column has the same letter repeated. For instance, the blocks of letters below show that ESARET is a rearrangement with no fixed letters of TERESA, but REASTE is not.
|
T |
E |
R |
E |
S |
A |
|
T |
E |
R |
E |
S |
A |
|
E |
S |
A |
R |
E |
T |
|
R |
E |
A |
S |
T |
E |
How many distinguishable rearrangements with no fixed letters does TERESA have? (The two E’s are considered identical.)
We can replace TERESA with 112345 because there are still six digits, with two being identical.
For a number that has no fixed digits with 112345, neither the first nor the second digit can be 1.
So, the first two digits can be any two of {2, 3, 4,
5}. There are 4P2
= 4 3 = 12 such permutations.
We will see how many numbers with no fixed digits with 112345 there are that begin with “23”
|
|
1 |
1 |
2 |
3 |
4 |
5 |
|
|
2 |
3 |
1 |
1 |
4 |
5 |
|
|
2 |
3 |
1 |
1 |
5 |
4 |
|
|
2 |
3 |
1 |
4 |
1 |
5 |
|
|
2 |
3 |
1 |
4 |
5 |
1 |
|
|
2 |
3 |
1 |
5 |
1 |
4 |
|
|
2 |
3 |
1 |
5 |
4 |
1 |
|
|
2 |
3 |
4 |
1 |
1 |
5 |
|
|
2 |
3 |
4 |
1 |
5 |
1 |
|
|
2 |
3 |
4 |
5 |
1 |
1 |
|
|
2 |
3 |
5 |
1 |
1 |
4 |
|
|
2 |
3 |
5 |
1 |
4 |
1 |
|
|
2 |
3 |
5 |
4 |
1 |
1 |
There are seven numbers that begin with “23” that have no fixed digits with 112345.
So the total number of required permutations is 12 7 = 84.
USAMTS Problem 2/3/13
Without computer assistance, find five different sets
of three positive integers {k, m, n} such that
k < m < n and .
Let us first consider all possible sets of two integers {a, b},
such that
So,
,
or
,
or
Now, if a and b are integers, then must also be integers.
Thus, are integer factors of 7056.
So, the possible pairs are:
|
{2, 3258} |
{21, 336} |
|
{3, 2352} |
{24, 294} |
|
{4, 1764} |
{28, 252} |
|
{6, 1176} |
{36, 196} |
|
{7, 1008} |
{42, 168} |
|
{8, 882} |
{48, 147} |
|
{9, 784} |
{49, 144} |
|
{12, 588} |
{56, 126} |
|
{14, 504} |
{63, 112} |
|
{16, 441} |
{72, 98} |
|
{18, 392} |
{84, 84} |
By substituting these values in for ,
we find that the only pair that produces integer values for a and b is {49, 144}.
{49, 144} gives us a = 7 and b = 12.
So, .
Now, we can find all integers {c, d} such that ,
and all integers {e, f} such that
.
This will give us numbers in the form and
,
which satisfy our given conditions.
So,
,
or
,
or
Possible values for (c 7) and (d
7) are {1, 49} and {7, 7}
If we don’t want c to equal d, then the only solution is c = 8 and d = 56.
So, ,
or {8, 12, 56} is one value for {k, m, n}
Now we will find all integers {e, f} such that
,
or
,
or
Possible values for (e 12) and (f
12) are:
|
{1, 144} |
|
{2, 72} |
|
{3, 48} |
|
{4, 36} |
|
{6, 24} |
|
{8, 18} |
|
{9, 16} |
|
{12, 12} |
If we don’t want e to equal f, the solutions for e and f are:
|
e = 13 |
f = 156 |
|
e = 14 |
f = 84 |
|
e = 15 |
f = 60 |
|
e = 16 |
f = 48 |
|
e = 18 |
f = 36 |
|
e = 20 |
f = 30 |
|
e = 21 |
f = 28 |
Thus, {7, 13, 156}, {7, 14, 84}, {7, 15, 60}, {7, 16, 48}, {7, 18, 36}, {7, 20, 30},
and {7, 21, 28} are all valid values for {k, m, n}.
(In fact, there are many other solutions that can be found
by splitting differently.)
USAMTS Problem 3/3/13
Suppose p(x) = xn + an-1xn+1 + … + a1x + a0 is a monic polynomial with integer coefficients. [Here monic polynomial just means the coefficient of xn is one.] If (p(x))2 is a polynomial all of whose coefficients are non-negative, is it necessarily true that all the coefficients of p(x) must be non-negative? Justify your answer.
If we take
p(x) = x5
+ 100x4 + 100x3 x2
+ 100x + 100
we get
Here, p(x) is a monic polynomial with the coefficient of x2 being negative. All the coefficients of (p(x))2 are non-negative. Thus, it is not necessary for all the coefficients of p(x) to be non-negative for all the coefficients of (p(x))2 to be non-negative.
USAMTS Problem 4/3/13
As shown in the figure on the right, in ΔACF, B is the
midpoint of![]() , D and
E divide side
, D and
E divide side into three equal parts, while G, H, and I
divide side
into four equal parts. Seventeen segments are drawn to connect these
six points to one another and to the opposite vertices of the triangle. Determine the points interior to ΔACF at
which three or more of these line segments intersect one another. To make grading easier, we have embedded the
triangle into the first quadrant with point F at the origin, point C at
(30s, 30t), and point A at (60r, 0), where r, s, and t are arbitrary positive real numbers. Please use this notation in your solutions.
.
Using one specific triangle (see Fig. 1), I drew,
experimentally, the seventeen segments.
I found that there were only two likely cases of more than two lines
intersecting at a single point. These
are the intersection of![]() ,
, and
,
and the intersection of
,
,
and
. We will
prove that these triplets of lines do indeed intersect at single points.
(See proofs 1a and 1b) .
We will also prove that:
- The shape and size of the triangle does not matter when considering if the lines intersect at a single point or not. In other words one can take any arbitrary value for (r, s, t). (See proof 2) (Thus, In fact to simplify, one can use r=t=1, and s=0)
- Hence there are only two such common points in any triangle. (If the points clearly do not coincide in a particular case, they will not, in any other triangle)
- We will also show mathematically that these are the only two points. (See part 3)
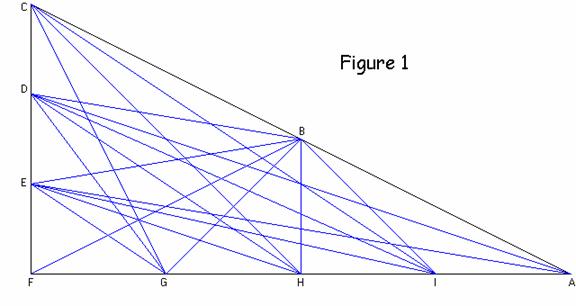
Using the given coordinate system, the coordinates of points A F are:
A(60r, 0), B(15s + 30r, 15t), C(30s, 30t), D(20s, 20t), E(10s, 10t), F(0, 0), G(15r, 0), H(30r, 0), and I(45r, 0)
Proof 1a:
We will show that ![]() ,
, ![]() , and
, and meet at one point.
The equation of is
= 20tx
1200rt …. (Eq 1)
The equation of is
= 15tx
450rt ……………(Eq 2)
The equation of is
= 30tx
1350rt …… (Eq
3)
By multiplying Eq 1 by 3 and subtracting Eq 2 multiplied by 4 we get for the point of
intersection for lines and
:
y(60s 180r
60s)
= -1800rt
or y = 10t
Similarly, by subtracting Eq 3 from 2 times Eq 2, we get for
the point of intersection of lines and
:
y(45r) = 450rt
or y = 10t
Since both points have same y value, we need not check the x value because none of the above lines are horizontal.
Thus the three lines intersect at one point
Substituting the value in Eq (1) we get x = 30r+10s and so the common point is,
(30r+10s, 10t)
Proof 1b:
We will show that, ,
,
and
meet at one point.
The equation of is
,
or
(s + 2r)y = tx ………… (Eq 4)
The equation of is
y(30s 15r) = 30t(x
15r) = 30tx
450tr, or
(2s r)y =
2tx - 30tr ………(Eq 5)
The equation of is
y(10s 30r)
= 10t(x
30r)
= 10tx
300tr,
or
(s 3r)y = tx - 30tr ………(Eq 6)
By subtracting Eq 4 from Eq 6, we get, for the point of
intersection of lines and
:
-y(s 3r)
+ y(s + 2r) = 30tr, or
y = 6t
By subtracting two times Eq 4 from Eq 5, we get, for the
point of intersection of lines and
:
-y(2s r) +
y(2s + 4r) = 30tr, or
y = 6t
Again, since both points have same y value, we need not check the x value because none of the above lines are horizontal.
Thus the three lines intersect at one point
Substituting the value of y in Eq (4) we get x = 12r + 6s,
So the common point is at
(12r+6s, 6t)
Proof 2:
Let and
be two intersecting lines in ΔACF. Let L
and N be the points on
where these lines meet at the base. (We will
later discuss the case where the end
points are not on the line AF) Let the
point of intersection be P.
Let us take the case where both K and M are on the line CF. (See Fig 2).
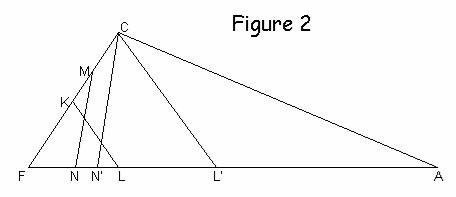
According to the problem, the values of and
are
given constants (they do not
depend on r, s, or t)
Now, let us draw a line parallel to through C,
and a line parallel to
through C,
meeting
at points L'
and N', respectively.
So,
ΔFKL ~ ΔFCL'
So, the values of and
are constants and hence
is also a constant.
Now
ΔPNL ~ ΔCN'L'
Thus, the height of ΔPNL is proportional to the height of ΔCN'L' . In other words, the height (or y-coordinate) of the point P depends only on the height of the original triangle, and not the shape.
![]() Using
similar logic, it is easy to see that this will hold true even if the point K is on
the line
Using
similar logic, it is easy to see that this will hold true even if the point K is on
the line ,
as long as the ratio of AK to AC is a given constant. Similarly, if
the two end points are on lines
AC and CF, one simply extends the line so that it meets the bases . (In the given problem there are no horizontal
lines, so the line will meet AF) . In all
the cases , the horizontal segments of the small and large triangles
would be proportional to the base of the triangle and the height would be
proportional to the height of the
original triangle.) See following figures
F
Here
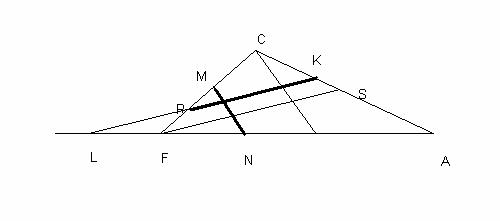
CS= (CF/RC)*CK ; SA= CA-CS ; and LA = (KA/SA)*FA and thus LA/FA is a constant (depends only on the given ratios)
This method also suggest an easy way to find the heights of the points of intersection, and thus one can calculate if more than two lines meet at a point. Each line now can be represented by two parameters. First lets us take, t=1, r=1, and s=0. The two parameters are: x- intercept of the line (We will call it p of the line) and the x-intercept of the line parallel to the line and passing through C, (We will call it q). Then the height of the point of intersection is :
(difference in p values)/(different in q values) * (Height of the triangle).
Part 3 -
Let us write for all these lines:
|
Line |
p value |
q value |
p/15 |
q/15 |
|
AD |
60 |
90 |
4 |
6 |
|
AE |
90 |
180 |
6 |
12 |
|
BD |
120 |
180 |
8 |
12 |
|
BE |
-60 |
-180 |
-4 |
-12 |
|
BF |
0 |
-60 |
0 |
-4 |
|
BG |
15 |
-30 |
1 |
-2 |
|
BH |
30 |
0 |
2 |
0 |
|
BI |
45 |
30 |
3 |
2 |
|
CG |
15 |
15 |
1 |
1 |
|
CH |
30 |
30 |
2 |
2 |
|
CI |
45 |
45 |
3 |
3 |
|
DG |
15 |
45/2 |
1 |
3/2 |
|
DH |
30 |
45 |
2 |
3 |
|
DI |
45 |
135/2 |
3 |
9/2 |
|
EG |
15 |
45 |
1 |
3 |
|
EH |
30 |
90 |
2 |
6 |
|
EI |
45 |
135 |
3 |
9 |
Note that we have added additional columns as (p/15 and q/15) ,as , we are only concerned with the ratio, and these values will make it easier to calculate:
Using the above values, we find that the “y” values of the points of intersection ( and multiplying the ratio by 30 to get the answer in the same form as before) we get:
The following table shows the y coordinates of all points of intersection:
|
AD |
BE |
40/3 |
AE |
CH |
6 |
BF |
CG |
6 |
BG |
DI |
120/13 |
CH |
DI |
12 |
|
AD |
BF |
12 |
AE |
CI |
10/3 |
BF |
CH |
10 |
BG |
EH |
15/4 |
CH |
EI |
30/7 |
|
AD |
BG |
45/4 |
AE |
DG |
60/7 |
BF |
CI |
90/7 |
BG |
EI |
60/11 |
|
|
|
|
AD |
BH |
10 |
AE |
DH |
20/3 |
BF |
DG |
60/11 |
|
|
|
DG |
EH |
20/3 |
|
AD |
CG |
18 |
AE |
DI |
4 |
BF |
DH |
60/7 |
BH |
CI |
10 |
DG |
EI |
8 |
|
AD |
CH |
15 |
|
|
|
BF |
DI |
180/17 |
BH |
DI |
20/3 |
|
|
|
|
AD |
CI |
10 |
BE |
CG |
150/13 |
BF |
EH |
6 |
BH |
EI |
10/3 |
DH |
EI |
5 |
|
|
|
|
BE |
CH |
90/7 |
BF |
EI |
90/13 |
|
|
|
|
||
|
AE |
BF |
15/2 |
BE |
CI |
14 |
|
|
|
CG |
DH |
15 |
|||
|
AE |
BG |
45/7 |
BE |
DG |
100/9 |
BG |
CH |
15/2 |
CG |
DI |
120/7 |
|||
|
AE |
BH |
5 |
BE |
DH |
12 |
BG |
CI |
12 |
CG |
EH |
6 |
|||
|
AE |
CG |
90/11 |
BE |
DI |
140/11 |
BG |
DH |
6 |
CG |
EI |
15/2 |
|||
(Lines that obviously do not intersect inside the triangle have been ignored.)
It is easy to see that the only triplets of intersecting lines that have the same y coordinate are ((AD, BH), (AD, CI), (BH, CI); y = 10), and ((BF, CG), (BF, EH), (CG, EH); y = 6)
The only points where three or more lines intersect in a way described in the problem are:
(30r + 10s, 10t) and (12r + 6s, 6t)
USAMTS Problem 5/3/13
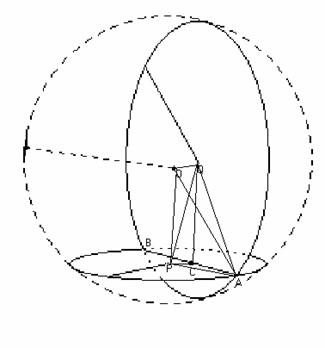
Two perpendicular planes intersect a sphere in tow circles. These circles intersect in two points, spaced 14 units apart, measured along the straight line connecting them. If the radii of the circles are 18 and 25 units, what is the radius of the sphere?
Let O be the
center of the sphere, and P and Q be the centers of the circles with
radii 18 and 25, respectively. Let the
circles meet at points A and B, and let C be the midpoint of .
So,
So,
Also, OQC =
QCP =
CPO =
PCA = 90
So,
Now, from right ΔOQA, we get
Thus, the length of
radius is 30.