Solving Differential Equations
Matlab has two functions, ode23 and ode45, which are capable of
numerically solving differential equations. Both of them use a
similar numerical formula, Runge-Kutta, but to a different order of
approximation.
The syntax for actually solving a differential equation with these
functions is:
[T,Y] = ode45('yprime',t0,tF,y0);
'yprime' is the name of a function that you write that describes your
system of differential equations. t0 and tf are the initial and final
times that you want a solution for, and y0 is a vector of the initial
values of the variables in your system of equations. You get back a
vector of times, T, and a matrix Y that has the values of each
variable in your system of equations over the times in the time
vector. Each column of Y is a different variable.
The hardest part of this is actually defining your differential
equation so that matlab understands it. Matlab has a very specific
way to define a differential equation, as a function that takes one
vector of variables in the differential equation, plus a time vector,
as an argument and returns the derivative of that vector. The only
way that matlab keeps track of which variable is which inside the
vector is the order you choose to use the variables in. You define
your differential equations based on that ordering of variables in the
vector, you define your initial conditions in the same order, and the
columns of your answer are also in that order.
If you follow a careful system to write your differential equation
function each time you need to solve a differential equation, it's not
too difficult. I'll do an example in this system to explain how it
works. In my example, x and y are functions of t.
The system of differential equations we're trying to solve is
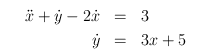 The first thing to notice is that this is not a first order
differential equation, because it has an
The first thing to notice is that this is not a first order
differential equation, because it has an 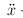 in it.
To create a function that returns a second derivative, one of the
variables you give it has to be the first derivative. So the
variables the function needs to start with are
in it.
To create a function that returns a second derivative, one of the
variables you give it has to be the first derivative. So the
variables the function needs to start with are 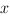 ,
, 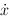 , and
, and 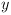 . The function needs to tell
matlab how to get from those variables to
. The function needs to tell
matlab how to get from those variables to 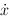 ,
, 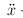 , and
, and 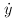 .
.
The first step is to write the first line of the function. Since x
and y are functions of t, and we eventually want the differential
equation to give us x and y, we'll define the function with
function dxy = diffxy(t, xy)
This function is called diffxy. That means it should be in a file
called diffxy.m
. It takes a vector xy (which has all three
of the variables we said we had to give matlab to define our
differential equation in it) and a time vector, and gives us the
derivative of the three things in the the xy vector.
The next step is to assign some variables from the xy vector that this
function is given. This is when we decide what order the three things
in the xy vector will be in. We could just keep calling them xy(1),
xy(2), and xy(3), but then we might forget which one of them was
supposed to represent x, which one was supposed to represent y, etc.
So the first thing we do is rename some variables:
x = xy(1);
xdot = xy(2);
y = xy(3);
Now we can use x, xdot, and y to define the three things that this
function has to return---xdot, xdoubledot, and ydot. This is where we
actually refer to the differential equation and implement it.
The first definition is trivial. We need to express xdot (the
derivative of x) in terms of the three variables we're given. xdot is
already one of the three variables we're given, so we can use it to
start with:
xdot = xdot;
Then xdoubledot comes from the first equation:
xdoubledot = 3 - ydot + 2*xdot;
Whoops, we don't _have_ a ydot yet. It's not one of the three
variables we're given in xy. But the second equation tells us what
ydot is equal to in terms of things we _are_ given in xy. So what we
really want to say is
ydot = 3*x + 2*y + 5;
xdoubledot = 3 - ydot + 2*xdot;
The last thing we want to define is ydot, which is the derivative of
y. We just defined it above in order to get xdoubledot, so we're
done.
So dxy, the thing we return, has to contain xdot, xdoubledot, and ydot
in order. The final thing we have to do is combine those values into
the vector dxy:
dxy = [xdot; xdoubledot; ydot];
Then we have a finished function that takes t and xy, and returns dxy,
which is the derivative of all the elements in xy. You can follow
this approach for any number of differential equations.
The final program, diffxy.m, looks like
function dxy = diffxy(t, xy)
%
%split xy into variables in our equations
%
x = xy(1);
xdot = xy(2);
y = xy(3);
%
% define the derivatives of these variables from equations
%
xdot = xdot;
ydot = 3*x + 2*y + 5;
xdoubledot = 3 - ydot + 2*xdot;
%
%return the derivatives in dxy in the right order
%
dxy = [xdot; xdoubledot; ydot]
To get a solution, we can type
[T, XY] ode45('diffxy',0,10,[0 1 0])
which uses times from 0 to 10 and assumes that the initial value of x
is 0, xdot is 1, and ydot is 0, and gives us a time vector and a three
column vector that contains values of x, xdot, and y over that time
vector.
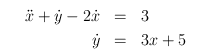 The first thing to notice is that this is not a first order
differential equation, because it has an
The first thing to notice is that this is not a first order
differential equation, because it has an 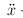 in it.
To create a function that returns a second derivative, one of the
variables you give it has to be the first derivative. So the
variables the function needs to start with are
in it.
To create a function that returns a second derivative, one of the
variables you give it has to be the first derivative. So the
variables the function needs to start with are 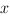 ,
, 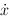 , and
, and 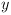 . The function needs to tell
matlab how to get from those variables to
. The function needs to tell
matlab how to get from those variables to 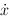 ,
, 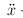 , and
, and 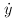 .
.