Extinction on a seascape
![]() For μ ≠ 0 and a≠0 the steady-steady distribution has natural cutoffs at small and large values
For μ ≠ 0 and a≠0 the steady-steady distribution has natural cutoffs at small and large values
_propt-4.jpeg)
However, the value of
must be computed self-consistently. Averaging the stochastic equations in the steady state gives
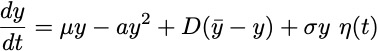
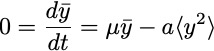 , leading to
, leading to
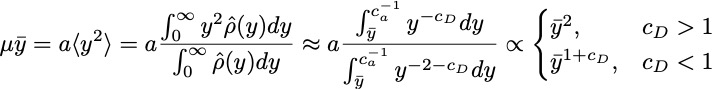 , and
, and
New universality class for extinction, with exponents continously varying with noise
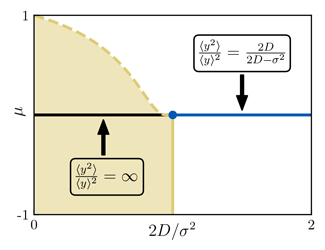
The phase transition has multi-fractal character, with distinct singularities for different moments, e.g.
![]() Demographic noise, however, changes the form of the distribution for y →0 :
Demographic noise, however, changes the form of the distribution for y →0 :
_=_y^--1.jpeg)
Averaging the stochastic equations in the steady state now leads to
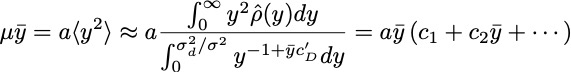
The extinction threshold is now shifted to a finite value
, close to which the mean population vanishes as
![]()
Standard mean-field (directed percolation) scaling is restored; with anomalous scaling above a crossover scale.