Random Matrix comparisons

   Random matrix theory: similarities and distinctions

 For an NxN random matrix, the top eigenvalues behave as

 The scaling with  N   suggests a correspondence:

 If such correspondence holds, for the free energy of m non-intersecting paths, we would get

 To reproduce the m^2 for free energy, we would need for eigenvalues of          to behave as

 Similar scaling  with  N=>t   as expected for DPRM, but different scaling with eigenvalue index. 

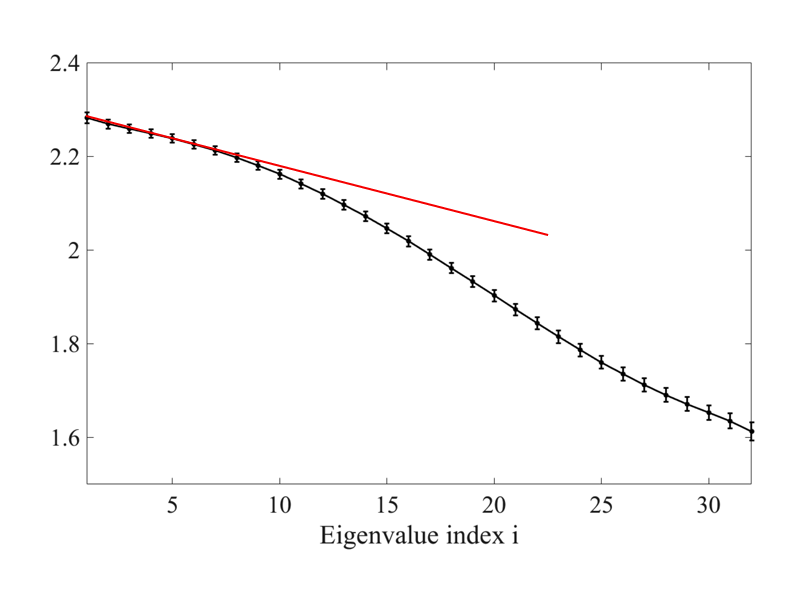
Sherry Chu, MIT thesis (2019) (offline) chapter

  Density of states: The scaling with eigenvalue index is a reflection of the scaling of density of states at the edge:

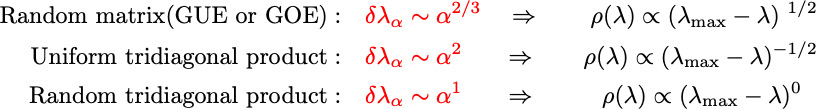
(Sidenote: while the product of tridiagonal random matrices is not symmetric, all eigenvalues remain real and positive!)

 Evolution of Log(eigenvalues) in "time":

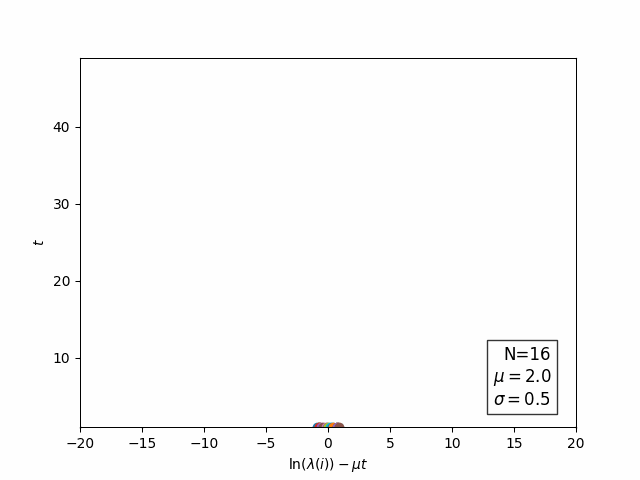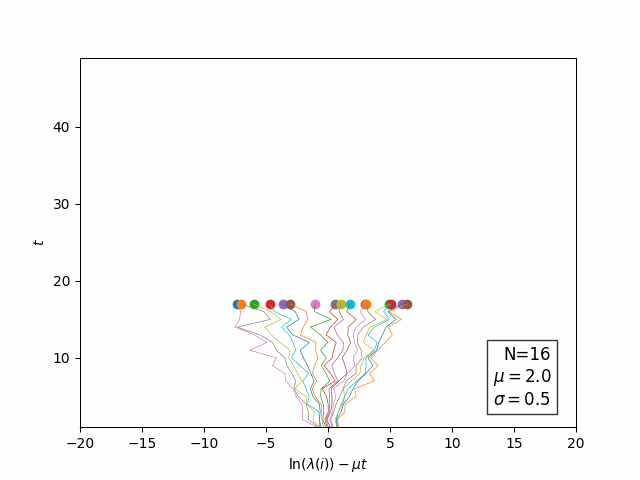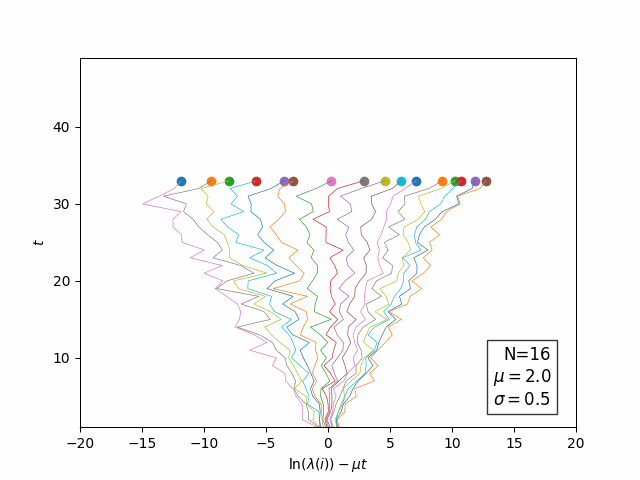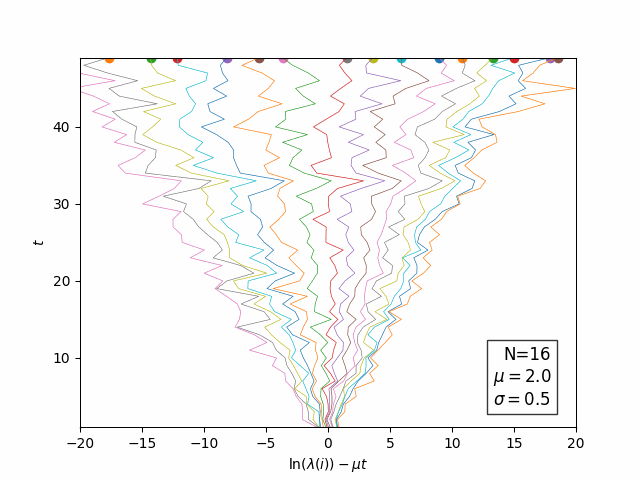
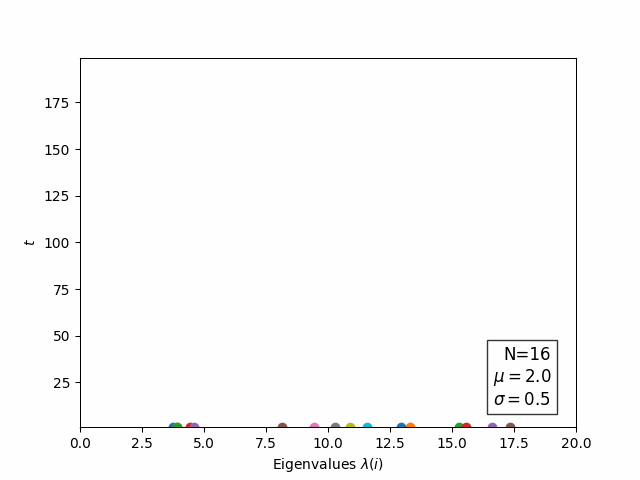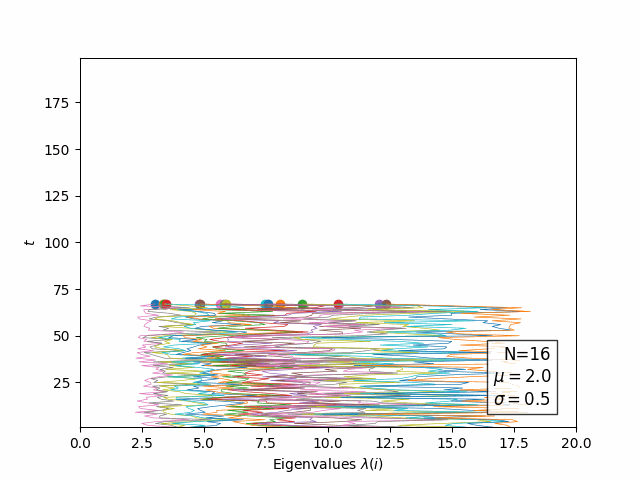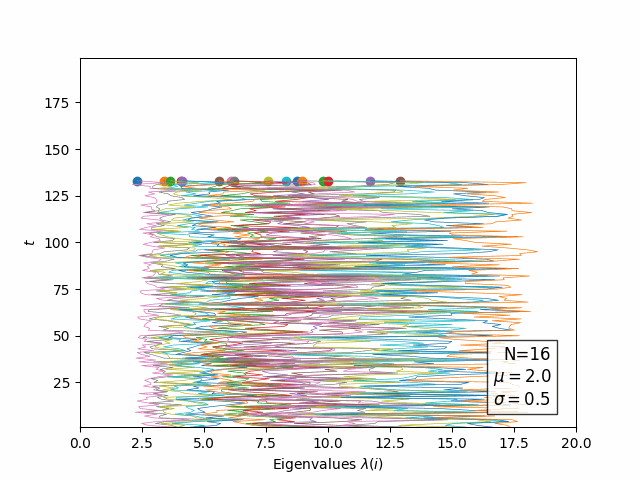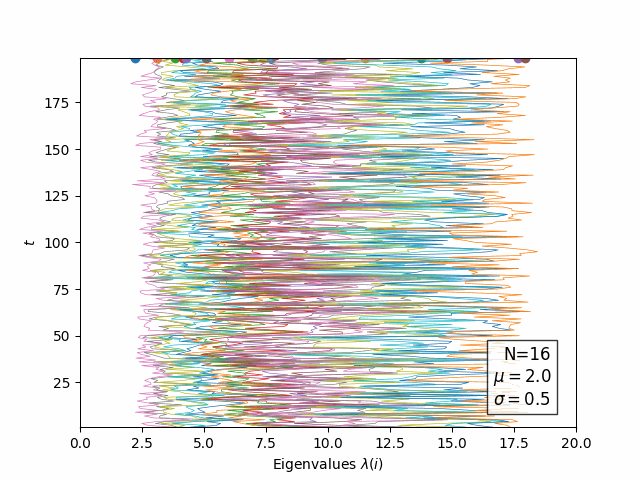
 Open questions:

 Transition between  and  .

 Transition between edge and middle Log(eigenvalues).

 "Particle-hole" symmetry between smallest and largest Log(eigenvalues).

 Is the arrangemet of Log(eigenvalues) hyperuniform?